Einen Sonderfall für die Dominanz stellen äquivalente Verbindungen dar. Zwei Verbindungen sind äquivalent, wenn sie sich lediglich in der Wahl der Umsteigehalte unterscheiden, ansonsten aber Gleichheit in Bezug auf die Abfahrtszeit und Reihenfolge der benutzen Fahrzeitprofile besteht.
Besitzen die Verbindungen Teilwege ohne Zeitlage (DRT, Sharing, ÖV-Zusatz), wird die Definition der Äquivalenz etwas angepasst: alle Teilwege ohne Zeitlage werden dann wie ein einziges Fahrzeitprofil behandelt. Darüber hinaus ist eine übereinstimmende Zeitlage dann gegeben, wenn jeweils der erste und letzte Teilweg, der mit einer regulären ÖV-Linie absolviert wird, dieselbe Fahrplanfahrt benutzen. Damit sind insbesondere Verbindungen der Art „DRT –> ÖV-Linie“ äquivalent, die in die gleiche Fahrplanfahrt an unterschiedlichen Haltestellen zusteigen.
Wird die Dominanz von äquivalenten Verbindungen erlaubt, so dominiert die Verbindung mit der höchsten Priorität (kleinster Zahlenwert) alle Verbindungen mit niedrigerer Priorität aus einem Bündel äquivalenter Verbindungen. Bei Gleichheit der Prioritäten legen Sie fest, ob die Verbindung mit dem frühest- oder spätestmögliche Umstieg verbleiben soll. Die Umsteigepriorität kann an Haltestellenbereichen und zwischen zwei Fahrten (geplante Anschlüsse) gesetzt werden. Die Prioritäten der Ebenen werden addiert, der Anschluss mit der höchsten Priorität (kleinster Zahlenwert) verbleibt als Verbindung. Für Haltestellenbereiche und geplante Anschlüsse gilt eine Standard- Priorität von „8“, die allen nicht definierten Elementen zugeordnet wird.
Wenn äquivalente Verbindungen zugelassen werden, kann eine große Menge fast identischer Verbindungen entstehen. Beachten Sie, dass Hierarchien innerhalb der Verbindungsmenge im Wahlmodell nicht berücksichtigt werden können. Durch Verwendung der Eigenständigkeit kann diese Tatsache in manchen Fällen kompensiert werden.
|
Hinweis: Eine Deaktivierung der Eigenständigkeit kann in Kombination mit äquivalenten Verbindungen zu unrealistischen Ergebnissen führen. Es wird daher dringend empfohlen, äquivalente Verbindungen nur mit der Option Eigenständigkeit verwenden zuzulassen. |
Beispiel
Betrachtet wird das in der Abbildung 164 dargestellte Netz.
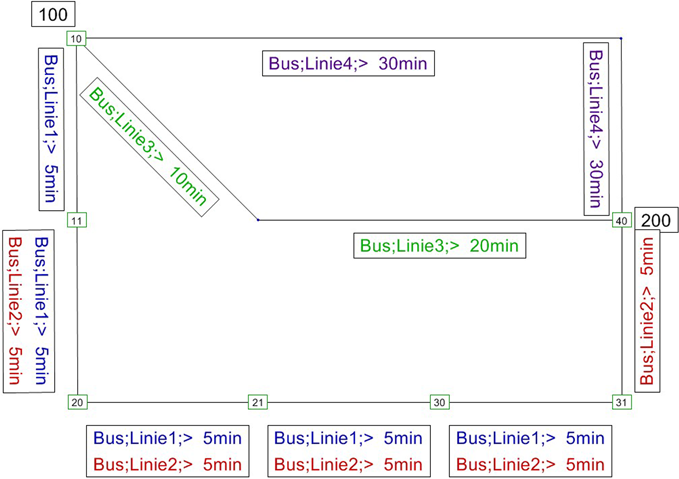
Abbildung 164: Beispiel äquivalente Verbindungen
Bei Nutzung der Linien 1 und 2 ergeben sich die folgenden äquivalenten Verbindungen:
| Verbindung | Von-Fahrzeitprofil | Nach-Fahrzeitprofil | Umsteigehaltepunkt |
|---|---|---|---|
|
A1 |
Bus, Linie 1 >, 1 |
Bus, Linie 2 >, 1 |
11 |
|
A2 |
Bus, Linie 1 >, 1 |
Bus, Linie 2 >, 1 |
20 |
|
A3 |
Bus, Linie 1 >, 1 |
Bus, Linie 2 >, 1 |
21 |
|
A4 |
Bus, Linie 1 >, 1 |
Bus, Linie 2 >, 1 |
30 |
|
A5 |
Bus, Linie 1 >, 1 |
Bus, Linie 2 >, 1 |
31 |
Wird Dominanz zwischen äquivalenten zugelassen, verbleibt nur die Verbindung A1
Beispiel mit Eigenständigkeit:
| Verbindung | Teilweg(e) |
|---|---|
|
A |
Abfahrt 6:30 mit Linie 1 Umstieg in Linie 2 im Überlappungsbereich der Halte 11, 20, 21, 30 und 31 mit UWZ = 0 Ankunft 7:00 |
|
B |
Abfahrt 6:35 mit Linie 3 Ankunft 7:05 |
|
C |
Abfahrt 7:00 mit Linie 4 Ankunft 7:30 |
Ohne Eigenständigkeit:
Ohne äquivalente Verbindungen erhält jede der drei Verbindungen einen Anteil von 1/3, wenn die Widerstandsparameter so eingestellt sind, dass der Umstieg nicht bestraft wird.
Werden äquivalente Verbindungen zugelassen, entstehen aus Verbindung A (mit Umstieg an Halt 11) vier weitere Optionen A2 bis A5, die sich nur im Umsteigepunkt unterscheiden. Die Verbindungsmenge besteht jetzt aus sieben gleich guten Verbindungen und ohne Eigenständigkeit erhält jede Verbindung 1/7 der Nachfrage. Dieser Fall illustriert, dass ohne Eigenständigkeit unrealistische Ergebnisse beim Wahlmodell entstehen.
Mit Eigenständigkeit:
Mit Eigenständigkeit verschiebt sich in der Ausgangssituation einige Nachfrage auf Verbindung C, weil A1 und B eine sehr ähnliche zeitliche Lage haben. C erhält nun 47%, die beiden anderen teilen sich den Rest.
Werden äquivalente Verbindungen zugelassen, ändert sich der Anteil von C kaum, aber ein großer Teil der Nachfrage verschiebt sich von B nach A, weil sich A1 bis A5 nicht nur gegenseitig beeinflussen, sondern allesamt auch die Eigenständigkeit von B reduzieren. An diesem Fall wird deutlich, dass Sie mit Verwendung der Eigenständigkeit bessere Ergebnisse erzielen, er macht aber auch die Grenzen der Eigenständigkeit deutlich.
|
Eigenständigkeit ausgeschaltet |
Eigenständigkeit eingeschaltet |
||
|---|---|---|---|
|
Äquivalente Verbindungen |
Äquivalente Verbindungen |
||
|
nein |
ja |
nein |
ja |
|
33,3 % |
71,4 % |
26,5 % |
41,8 % |
|
33,3 % |
14,3 % |
26,5 % |
10 % |
|
33,3 % |
14,3 % |
47 % |
48,2 % |

